Functors, Applicatives, and Monads

Unboxing Functional Programming Concepts

Hello! Today, we will explore functional programming with the concepts of functors, applicatives, and monads. We will discuss what they are and why they matter one step at a time. Note that all the examples will be in Haskell, but you’re not required to know Haskell to read this post.

I’ve also added a section at the end following a pretty disappointing interaction with someone associated with the Haskell foundation.

Functors

This is a closed box:

Of course, as with every closed box, you can’t really know what’s inside unless you open it, right? So let’s open it, and… surprise! The box contains the answer to the Ultimate Question of Life, The Universe, and Everything¹:

Now, let’s translate the box analogy into programming. A box can be any data structure surrounded by a context. Said differently, a wrapper or container type that adds additional information or behavior to the underlying data.

In this example, we will say that blue boxes represent the possibility of an optional value, which in Haskell is denoted by the Maybe type. But, this concept exists in many languages: Rust with Option, Go with sql.NullString, Java with Optional, etc.

Yet, other types of boxes also exist. For example:

• A box representing that the wrapped value can be either from one type or another. For example, in Haskell, Either to represent a value that is either Left or Right, or in Rust, Result to represent either a success or an error.

• More generally, most classic data structures we can think of such as lists, maps, trees, or even strings. Those data structures can contain zero, one, or multiple values inside. For example, a string can be composed of zero, one, or multiple characters.

We already know how to apply a function to a simple value; for example, applying a function that adds one to a given int:

Here, the white square represents a function that takes an integer and adds one to it.

But what if we want to apply the same function to a value inside a box? We could open the box, extract the value out of it, apply the function, and put the result back in a box:

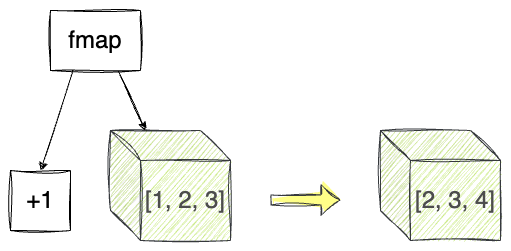
Yet, in Haskell, we can use fmap to apply a function to a box directly; no need to perform all the steps ourselves:

fmap is used to apply a transformation function, here (+1), to the value inside a box and put the result inside another box.

In this example, the box itself is called a functor. A functor is an abstraction that allows for mapping a function over values inside a context without altering the context of the functor.

Not altering the context is crucial; a functor is not similar to the box in Schrödinger’s experiment. In quantum physics, opening a box alters the state of what’s inside. Here, this is not the case: the box with the value 42 remains identical².

Examine the Haskell code for this example:

fmapEx :: Maybe Int -- A function returning a Maybe Int
fmapEx = fmap (+ 1) (Just 42) -- Result: Just 43

If you’re unfamiliar with Haskell, let’s spend 30 seconds on this snippet. The first line defines the signature of fmapEx, a function that takes no input and produces a Maybe Int output. The second line represents the core logic of the function: applying the (+1) transformation function to Just 42. Here, Maybe is a box type, while Just 42 is an instance of this box with the value 42 inside.

As we said, a box can either contain a value or be empty, so what happens if we apply the (+1) transformation to an empty box? The result is also an empty box:

Indeed, applying (+1) to a non-existent value doesn’t give 1. You can’t increase your bank account balance if you don’t have a bank account; the same is true in Haskell.

Here’s the code for this new example:

fmapEx :: Maybe Int
fmapEx = fmap (+ 1) Nothing -- Result: Nothing

Nothing means a Maybe box with no value inside.

We also said that the box analogy can be applied to other data structures; for example, a list of values. Let’s use green boxes to represent lists of elements. We can reuse fmap to apply the (+1) function to every list’s elements:

fmapEx :: [Int] -- A function returning a list
fmapEx = fmap (+ 1) [1, 2, 3] -- Result: [2, 3, 4]

Pretty handy, right? Instead of looping manually over each element and creating a new list, we can provide a transformation function to fmap and Haskell will handle the rest for us.

That’s the essence of functors: an abstraction representing something to which we can apply a function to the value(s) inside. Yet, in the next section, we will see that functors are somewhat limited and why we need an upper-level abstraction: applicatives.

Applicatives

What if instead of applying a transformation function to a box, we wanted to apply a transformation function inside a box:

Here, (+1) is wrapped in a Maybe box. In that case, using fmap and functors, that’s a compilation error:

fmapEx :: Maybe Int
fmapEx = fmap (Just (+ 1)) (Just 42) -- Does not compile

Indeed, the fmap function only works if the transformation function is outside of any box.

But hold on… We haven’t yet discussed the purpose of a function inside a box.

A few examples:

• When we want to represent a situation in which a function is optional or may be missing (e.g., due to an error or incomplete computation), we can represent it using Maybe.

• When we want to handle a variable number of functions, we can put these functions in a list.

Now that we understand why functions inside boxes are a possibility, let’s discuss how to handle this case:

The solution is to switch to another type: applicative functors, also called applicatives in short. In this case, we must use in Haskell the <*> operator with applicatives:

Thanks to the <*> operator, we can now apply the (+1) function inside a Maybe applicative to the value inside another Maybe applicative.

A small note: have you noticed that we referred to <*> as an operator? In Haskell, an operator is also a function, but written in infix notation, meaning placed between its arguments:

applicativeEx :: Maybe Int
applicativeEx = Just (+ 1) <*> Just 42 -- Result: Just 43

Now what happens if we try to use <*> on two different applicative types? For example, a Maybe Int and a list of Int:

In this case, that’s a compilation error. Applicatives are also there for safety reasons; the context has to be the same to use the <*> operator. Yet, if the transformation function is inside a list as well, it works:

And what happens if we have multiple transformation functions in the first box and multiple values in the second box? Haskell applies the combination of each transformation function on each value:

So that’s what an applicative is: another abstraction that allows for applying functions wrapped in a context to values in the same context.

One last thing: what if a transformation function remains outside of a box?

Should we put this function inside a box? Should we turn the applicative into a functor to apply fmap? None of these is required. We can use the <$> operator, basically the fmap version for applicatives:

It illustrates that an applicative is an extension of a functor as it can cover both cases (in these examples A and B are generic types):

• If the function is outside a box, we can use the <$> operator:

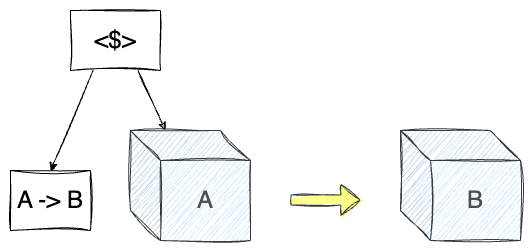
<$> takes an A to B function, applies it to the value inside an applicative, and puts the result inside another applicative.

• And if the function is inside a box, we can use the <*> operator:

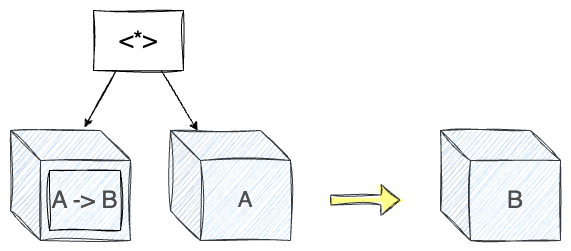
<*> takes an A to B function inside an applicative, applies it to the value inside an applicative, and puts the result inside another applicative.

Yet, like functors, we will also see that there’s a limit to how applicatives are helpful. Now, it’s time to move on to the final boss: monads.

Monads

So far, we have tackled two kinds of transformation functions (again, A and B are generic types):

• Functions outside a box:

A function taking an A as input and producing a B.

-- For example:
plusOne :: Int -> Int
plusOne x = x + 1

• And functions inside a box:

  

  Same, but this function is inside a Maybe box.

-- For example:
plusOne :: Maybe (Int -> Int)
plusOne = Just (+ 1)

But what if a function takes a value outside a box, applies a transformation, and puts the result inside a box?

For example:

First, let’s discuss the how and then the why of such a function.

There are two ways to do it in Haskell. We can use Just as we want to return a Maybe Int:

plusOne :: Int -> Maybe Int
plusOne x = Just (x + 1)

This function takes the x outside a box and puts the sum of x + 1 inside a Maybe Int box.

But there’s a second alternative that does exactly the same thing, this time using return:

plusOne :: Int -> Maybe Int
plusOne x = return (x + 1)

If you don’t know Haskell, you may be confused by this code. It’s worth knowing that return is a function that wraps something (an int, a function, whatever) inside a box. Thanks to type inference and the function signature, Haskell knows that return applied on (x + 1) should put this value inside a Maybe Int. We will come back later to the essence of what return is in Haskell.

Now, let’s move on to the why. Why does a function accept a value outside a box and return a value inside a box? For example, consider the case of a divide function that tackles the case if a denominator is zero:

divide :: Float -> Float -> Maybe Float
divide _ 0 = Nothing
divide x y = return (x / y)

This function accepts two Float and returns a Maybe Float. It uses pattern matching:

• If the denominator is 0, it returns Nothing (line 2)

• Otherwise, it returns the result of x / y inside a Maybe Float box (line 3)

divide illustrates a function accepting inputs outside boxes and returning a value inside a box.

Now let’s get back to our initial problem: Can an applicative work with a function that returns a value inside a box? Let’s give it a try.

The Limitation of Applicatives

Let’s implement a concrete scenario. We want to implement a function that receives a person's age and name. We want to greet the person only if he’s over 18 years old. For example:

• Providing “John” and 30 to our function should return a Maybe String box with “Hello John”:

• Yet, with an age of 16, for example, the function should return Nothing:

Let’s first introduce the two utility functions to validate the age (validateAge) and greet the person (greet):

validateAge :: Int -> Maybe Int
validateAge age
  | age >= 18 = return age
  | otherwise = Nothing

greet :: String -> String
greet name = "Hello " ++ name

validateAge uses Haskell’s guards syntax (|), a notation to define functions based on predicate values:

• If the age is above 18, we put it inside a Maybe Int

• Otherwise, we return Nothing

Regarding the greet function, it concatenates “Hello” and the person’s name using the ++ operator.

Back to applicatives, one could be tempted to write the function this way (remember, <$> is for functions outside a box, and <*> is for functions inside a box):

withApplicative :: Int -> String -> Maybe String
withApplicative age name = greet <$> Just name <*> validateAge age

Yet, this code doesn’t compile. Let’s understand why.

The first part of the expression (the part to the left of <*>) is OK and compiles as greet is a function outside a box and Just name is a value inside a box (a Maybe type):

As a result, it produces a function taking a String and producing a Just String:

The second part of the expression (the part to the right of <*>) is a Maybe Int:

Now, taking the whole expression, it gives us the following:

Yet, this code doesn’t compile:

Expected: String -> Int -> String
Actual: String -> String

Indeed, we discussed previously what kind of function is expected by the <*> operator (a function inside a box):

In this case, we can’t provide the type expected by <*> for the transformation function. So, we can’t make it work with applicatives (at least easily). We need something else.

Monads to the Rescue

To solve our problem, we can use monads and introduce a new operator, >>=:

This operator takes:

• A value of type A inside a box

• A function that transforms an A type into a B type inside a box

As a result, it produces a B inside a box. For instance:

This example in Haskell:

plusOne :: Int -> Maybe Int
plusOne x = return (x + 1)

monadEx :: Maybe Int
monadEx = Just 42 >>= plusOne -- Just 43

This is the first use case of monads: applying a transformation function that returns a value inside a box to a value inside the same box type.

Now, let’s get back to our problem (greeting if a person is over 18) and understand how to solve it using monads and the >>= operator:

withMonad :: Int -> String -> Maybe String
withMonad age name = validateAge age >>= \_ -> return (greet name)

Note that the code here uses a lambda function. A lambda in Haskell is an anonymous function using the \ notation. For example, \x -> x + 1, which increments its input x by 1. In the previous code, the lambda represents a function that takes an Int (because validateAge age is a Maybe Int) and returns a Maybe String.

This is what our code looks like with the >>= operator:

There’s one small thing that we could be bothered about. The transformation function passed to >>= takes an Int but doesn’t use it. This is the purpose of _, a placeholder to express that we want to ignore this parameter. Could we do better? Yes!

To solve the same problem without a clumsy lambda expression that doesn’t even use its input, we can use the do notation:

withMonad :: Int -> String -> Maybe String
withMonad age name = do
  validateAge age
  return (greet name)

The behavior of this code is the same as the previous one when we used the >>= operator:

• If validateAge age returns Nothing (when the age is under 18), the whole function returns Nothing. The computation terminates line 3 without further evaluation.

• Otherwise, it returns a string inside a Maybe.

Using the do notation, monadic expressions are written line by line. It may look like imperative code, but it’s just sequential, as each value in each line relies on the result of the previous ones and their contexts. do is used as a convenient way to sequence and compose monadic computations:

• Sequence: Take any traversable data structure (e.g., a list or a tree) of monadic values and transform it into a monadic value of the same data structure. For instance, [Just 1, Just 2, Just 3] into Just([1, 2, 3]):

• Compose: The act of combining two or more monadic functions together to create a new monadic function.

Remember about return? We said previously that return was used to wrap a value inside a context. More specifically, return wraps the value inside a monad; it does not end the function execution.

For example, what if we want to use the Maybe String value after return (greet name)? In Haskell, we can use <- to bind the result of a monadic action to a variable:

withMonad :: Int -> String -> Maybe String
withMonad age name = do
  validateAge age
  s <- return (greet name)
  return (greet s) -- Result: Just "Hello John"

Notice the multiple uses of return. As we said, in Haskell, return doesn’t stop the function execution; instead, it wraps a value inside a monad.

Summary

In summary, a monad is a powerful abstraction that extends the capabilities of applicatives. Monads provide a way to sequence and compose actions while preserving their contexts.

In Haskell, leveraging tools such as the do notation and the <- operator to bind variables, or return to wrap values inside monads allows developers to craft code that is not just concise but also remarkably powerful.

The concept of monads in Haskell goes beyond the limited scope of what we have discussed. Even I/O operations are encapsulated within monads. It allows impure actions (e.g., writing a file or reading a socket) to coexist within a purely functional framework. The monadic structure enables the sequencing and combination of I/O operation alongside any other monads.

Edit: The "Fatal Error"

I asked for a review from someone associated with the Haskell Foundation, but this person told me that writing about monads was a “fatal error”. This person also sent me The “What Are Monads?” Fallacy link and ended up denigrating my work on their own blog:

Writing a Monad Tutorial™ 2 minutes after having developed your own intuition for monads does not make one qualified for teaching anything. Intuition is something that is very personal, built by a person’s practice of a subject. Trust us, we know. (sic)

First of all, I am not expecting you to be able to use monads in your daily work only with this post. Obviously, it would require practice; I think we can all agree with that.

However, this interaction left me quite disappointed. For instance, I know the Go programming language pretty well. If a beginner in this language wanted to write about goroutines, that wouldn’t be my call to tell him that it’s a mistake because they’re not qualified enough. Absolutely not. And I could have created the Go language itself that my opinion wouldn’t change.

One could even argue that sometimes, beginners are even more conducive to better help than experts:

The fellow-pupil can help more than the master because he knows less. The difficulty we want him to explain is one he has recently met. The expert met it so long ago he has forgotten. He sees the whole subject, by now, in a different light that he cannot conceive what is really troubling the pupil.

C. S. Lewis

Everyone starts as a beginner. I think that in any community, it’s important to create an environment where people feel encouraged to learn and share. If my post gets someone to explore Haskell, that’s already a win, regardless of what others think about my “qualifications”.

📚 Resources

More From the Coding Category

• Partially Applied Functions vs. Currying

• Concurrency vs. Parallelism

• Coroutines

Source

• All About Monads

Explore Further

• A Fistful of Monads

1. Who could have thought with such a small box?

2. If we think about it, that’s a good thing, right? The answer to life shouldn’t be changed just by looking at it.